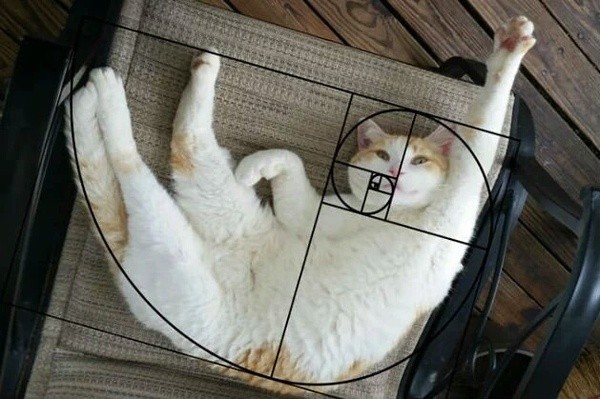
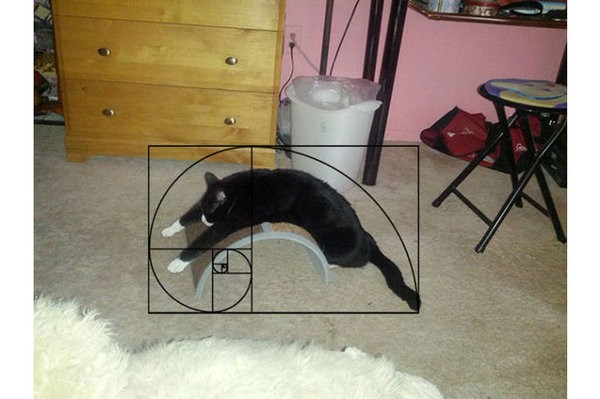
Оказывается Фибоначчи повсюду!
На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.
Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.
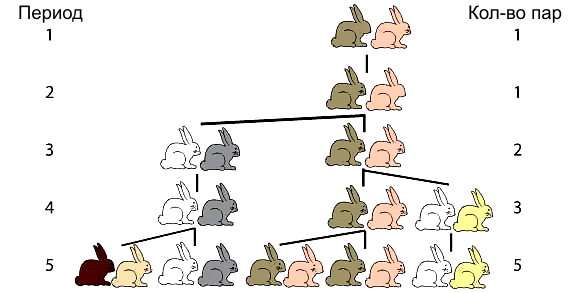
Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
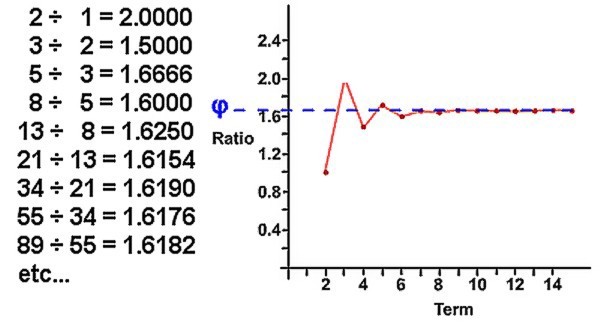
Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.
Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
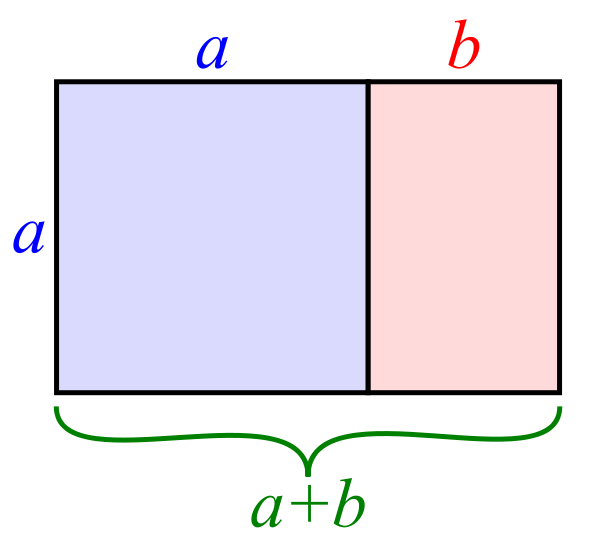
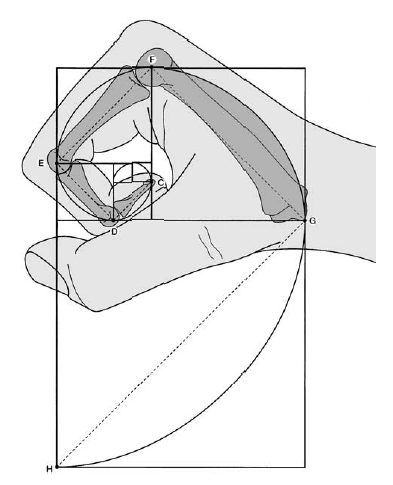
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.
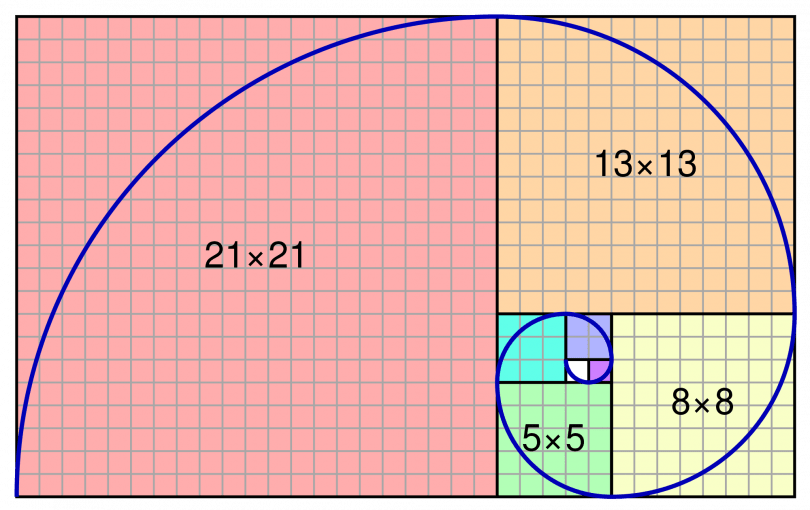
Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.
Числа Фибоначчи в природе
Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.

Последовательность Фибоначчи можно также увидеть в форме или разделении ветвей дерева. Основной ствол будет расти до тех пор, пока он не создаст ветвь, которая создает две точки роста. Затем один из новых стеблей разветвляется на два, в то время как другой находится в состоянии покоя. Такая картина ветвления повторяется для каждого из новых стеблей. Корневая система и даже водоросли также демонстрируют эту закономерность.
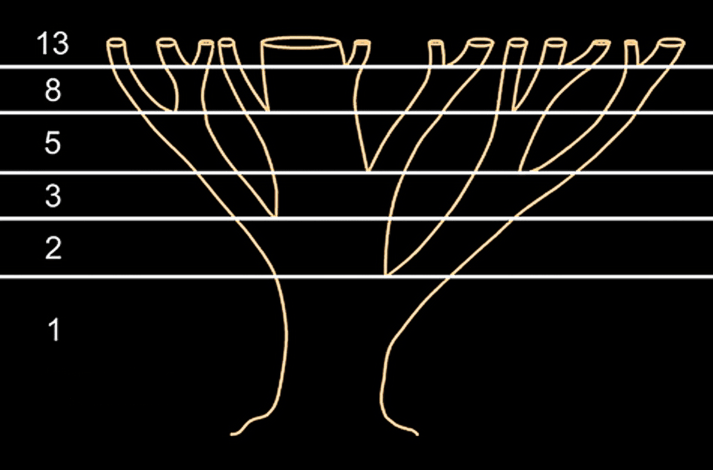
Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.

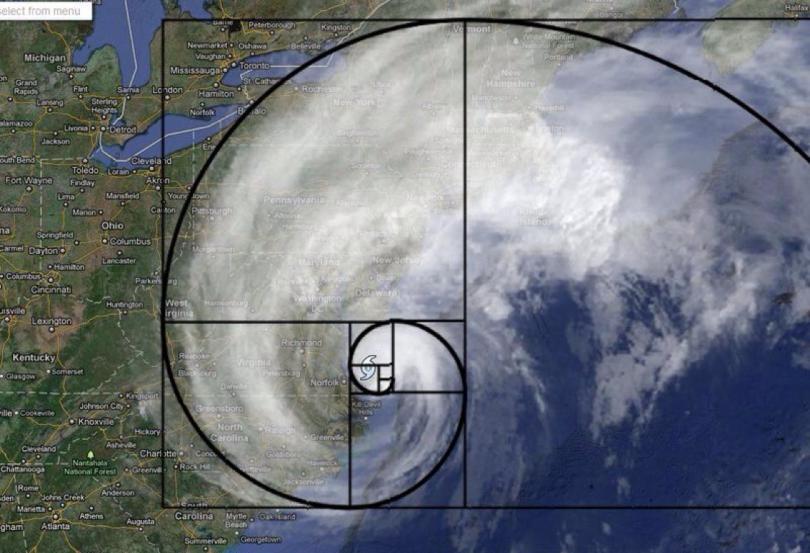

Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.

Числа Фибоначчи в теле человека
Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.
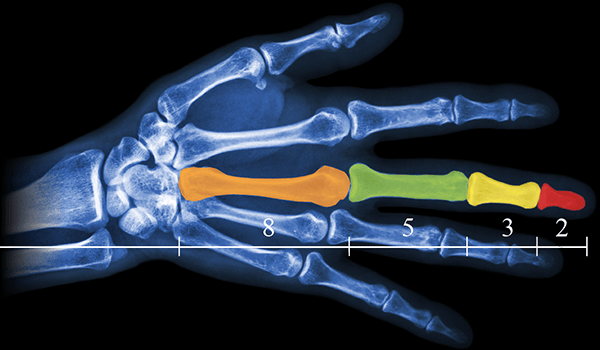
Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.
Числа Фибоначчи в биржевой торговле
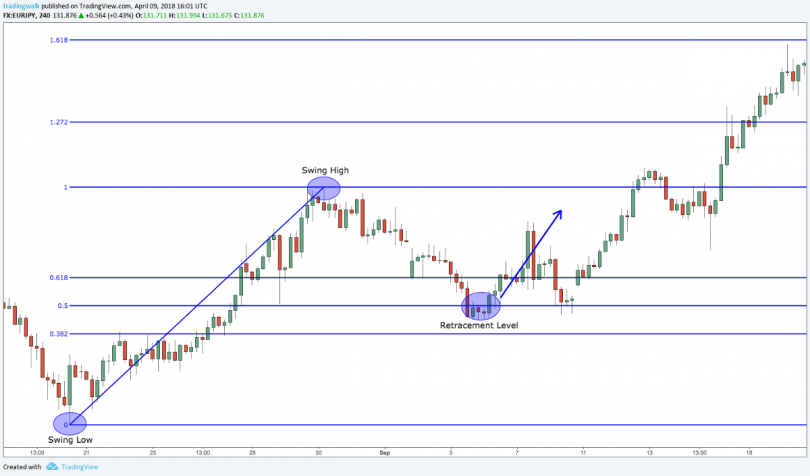
Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.
Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.
Числа Фибоначчи в фотографии и искусстве
В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.
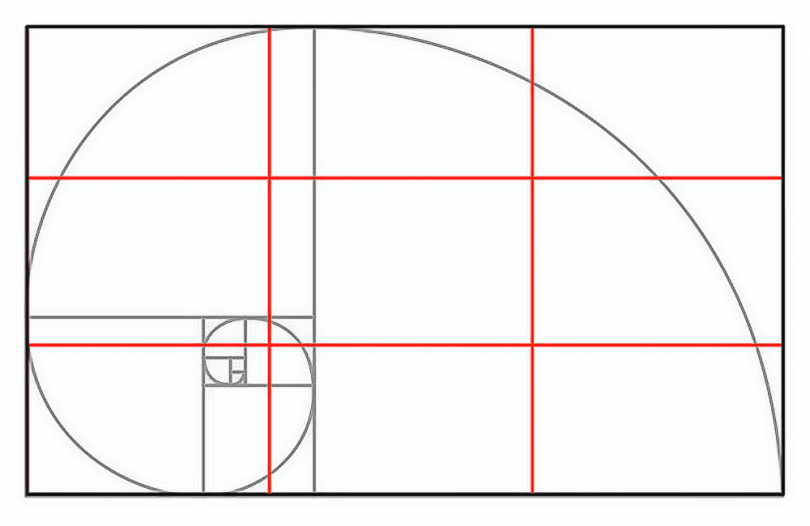
Сетка фи (красные линии) и спираль Фиббоначи в кадре.

Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.
Может именно из-за этого Дональд Трамп был избран президентом? (шутка):

И еще немного фундаментального числа!